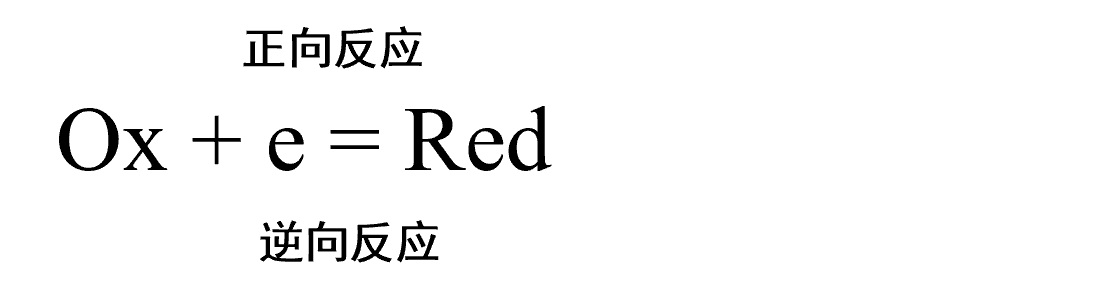
在上述反应情况下，假设在电极的表面氧化剂的浓度为COx，频率因子为 A，则上述反应的正向反应速率 vf可以用式26表示。

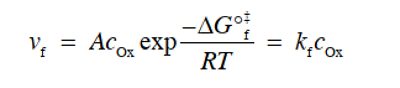
当电位差Δφ存在于电极-电解质溶液界面时，从电极到溶液中氧化物Ox的电子转移会受其影响。
在图7(c)中，假设电势梯度可以线性逼近，从反应坐标的起始状态侧看，能量曲线的峰值在划分为α：1-α的位置。 此时，需要额外的活化能αFΔφ才能从初始状态到达能量曲线的顶部。 因此，此时的反应速率 vf 可以通过将式（26）中的 ΔG°‡f 改成ΔG‡f 来重新排列得到式28

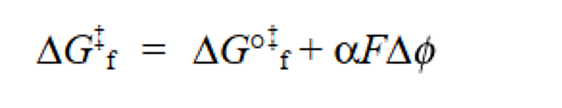
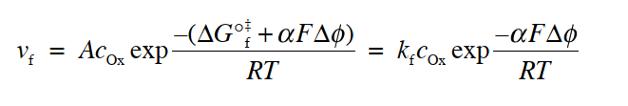
反应速度vf是单位时间内每单位面积发生反应的氧化态物质Ox的物质量，所以如果将每摩尔的电量F乘以vf，即为单位面积的还原电流（阴极电流, cathodic), 即, 阴极电流密度可改写为ic（下标“c”表示阴极）的式29，

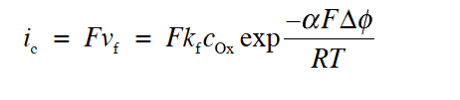
因此，在电化学中，必须始终牢记与电极反应相关的电流（也称为法拉第法拉第电流）对应于反应速度。 根据类似的论点，逆向的反应速率 vb 和阳极电流密度 ia可以表示为式30

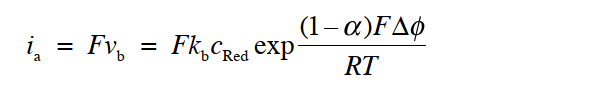
假设反应在电极表面上达到平衡状态。 即正向和反向的反应速度相等（vf=vb），换句话说，就是阳极电流密度和阴极电流密度相等（ic=ia），通过界面的净电流密度为零。且电位差 Δφ 用平衡电位差 Δφeq 表示，enter↓ 　将此时的电流密度用 i0 （ic=ia）来表示，则可以得到式31。

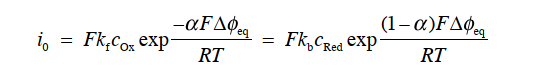
这里 i0 称为交换电流密度，从它是 kf 或 kb 的函数可以看出，它是一个反映电极反应动力学特性的指标。 i0 会发生多个数量级的变化，这不仅取决于反应类型（即氧化还原与 Ox / Red 的类型）和温度，还取决于电极材料及其表面状态。

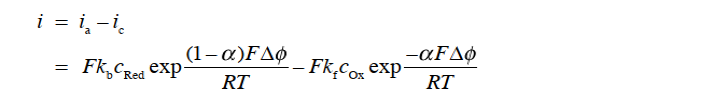
其中 Δφ 是非平衡时电极-电解质界面上的电位差。 式（32）简单说明了电极反应的电流相对于两点之间的电位差（M ΔSφ）呈指数变化即，与欧姆定律的线性关系不同。这是因为该等式包括电位差Δφ，这是一个无法实际测量的值。 我们只能测量电位差Δφ的变化和差异。 因此，我们将这个Δφ分成平衡电位差Δφeq 及其变化量η（=Δφ-Δφeq ）来进行考虑。
这种变化量称为过电位（over potential），其可以使用参比电极进行测量 式（33）。

这里，Eeq是使用参比电极测量的氧化还原对 Ox / Red 的平衡电极电位。 将从式 (33)中得到的Δφ = Δφeq+ η 的关系式，代入式 (32) 并利用式 (31) 的关系，得到式34。

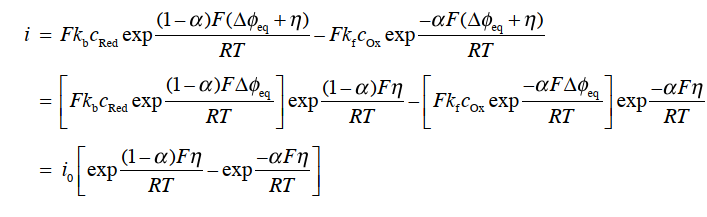
该方程（34）是描述净电流密度（即净电极反应速度）是如何随着，与平衡电位的偏差 η（过电位）而变化的基本方程，称为 Butler-Volmer 方程。