第二篇 电极反应动力学(2):电流和电位的关系
我们知道需要过电位才能使反应向一个方向进行。 那么,过电位的大小与实际观察到的电流之间存在怎样的关系呢?
前面已经多次提及电流是表示反应速率的指标。 另一方面,可以说电势起到调节反应能量平衡的作用。 在均相化学反应中,放热反应或吸热反应是由反应物体系能量与产物体系能量的大小关系决定的。 类似地,在电化学反应中,是否可以将能量向外部输出(电池),或 是否需要从外部提供(电解)是根据反应物体系和生成物体系之间的能量差异来确定的。 在这里,让我们从能量的角度考虑电势对电极反应的影响。
前面已经多次提及电流是表示反应速率的指标。 另一方面,可以说电势起到调节反应能量平衡的作用。 在均相化学反应中,放热反应或吸热反应是由反应物体系能量与产物体系能量的大小关系决定的。 类似地,在电化学反应中,是否可以将能量向外部输出(电池),或 是否需要从外部提供(电解)是根据反应物体系和生成物体系之间的能量差异来确定的。 在这里,让我们从能量的角度考虑电势对电极反应的影响。
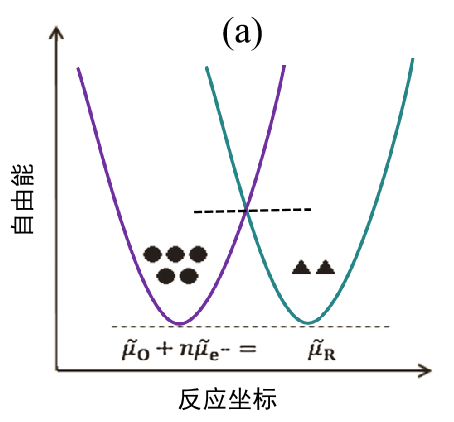
(a) 起始状态(平衡状态);
在平衡状态下反应物体系与产物体系的自由能相等。显然,反应不会向任何一个方向进行,所以 I = 0。 ● 和▲ 标记代表O 和R 的浓度大小。 请注意,平衡并不意味着浓度相等。
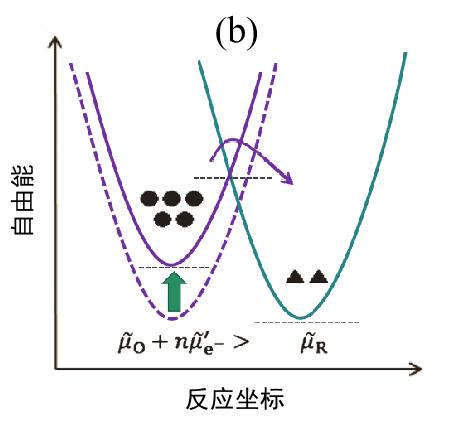
图 2. 电子转移反应能量示意图。
(b)施加负的过电压时(过渡状态);
对(a)的状态施加负的过电位时,电极内电子的能量增加,反应体系的自由能出现▣暂时性升高,O→R方向与R→O方向的反应活化能发生改变,反应向右侧进行而产生电流的流动(I < 0)
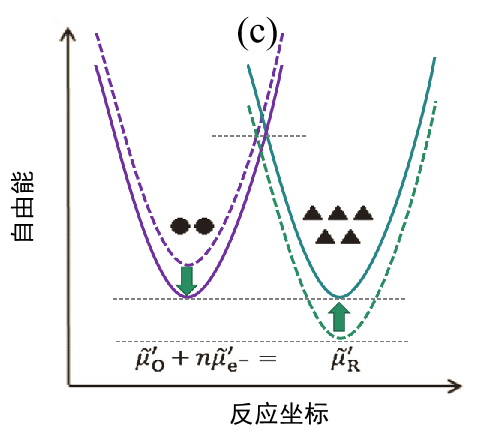
(c)最终状态(平衡状态)。
随着反应的进行,反应体系和生成体系之间的自由能差越来越小。 同时,活化能的差异也被消除,因此电流值减小,当 I = 0 时系统达到新的平衡。
如果起始状态处于平衡状态,两个体系的自由能相等图2(a)。 在这种状态下,对电极施加负过电压时,电极内部的电子能量增加,反应体系的自由能增加。反应体系的自由能出现暂时性升高然后,O →R 还原方向的反应活化能比以前减少,因此反应倾向于向右进行而产生电流的流动(I < 0), 此时相反的R→O氧化反应方向的活化能则增加(图2(b))。 随着 O 的消耗和 R 的增加,每个体系的能量也会发生变化,并且经过很长一段时间后,两者最终会变得相等。此时,反应显然已经停止,体系处于新的平衡状态(图2(c))。
从上面可以看出,当体系处于能量不稳定的非平衡状态(过渡态)时,可以观察到电流。
电化学反应的独特之处在于反应的方向可以通过施加在电极上的电位来控制。
当向电极施加与前一个相反方向的正过电位时,就会发生与上述相反的现象,此时反应从右向左进行,即氧化反应。 换言之,活化能的大小关系根据所施加的过电位的符号而反转。
与一般的化学反应类似,电化学反应的反应速度常数 k 是根据 Arrhenius 方程随活化能 Ea 变化的量。
从上面可以看出,当体系处于能量不稳定的非平衡状态(过渡态)时,可以观察到电流。
电化学反应的独特之处在于反应的方向可以通过施加在电极上的电位来控制。
当向电极施加与前一个相反方向的正过电位时,就会发生与上述相反的现象,此时反应从右向左进行,即氧化反应。 换言之,活化能的大小关系根据所施加的过电位的符号而反转。
与一般的化学反应类似,电化学反应的反应速度常数 k 是根据 Arrhenius 方程随活化能 Ea 变化的量。
(R :气体常数,T :绝对温度,A :系数)
当产生过电位η时,氧化反应与,还原反应的活化能可以分别用式11和式12来表示。
这里,Eaeq 是平衡电位处的活化能,阿尔法为传递系数的量(transfer coefficiency),氧化或还原反应的传递系数间存在着0 <αox, αred <1 和 αox+ αred =1 的关系。(传递系数是表示 施加的过电位对氧化或还原反应活化能变化的贡献率)。
根据上述关系,各反应速率常数表示如下。
根据上述关系,各反应速率常数表示如下。
式13表示了氧化反应速度常数, 式14表示了还原反应速度常数。式中的keq 为平衡电位处的反应速度常数。从上述方程可以看出,反应速度,即电流,与电位的变化呈指数依赖关系。 这种过电位称为活化过电位(activation overvoltage, or activation overpotential)或称超电势。
最初通过实验发现了电解电流和外加电压之间的指数关系,并将两者之间的关系进行表述的是著名的塔菲尔方程。
如上所述,从理论上考虑活化能和过电压之间的关系并将其与反应速率(电流)定量关联的方程为Butler-Volmer 方程。
最初通过实验发现了电解电流和外加电压之间的指数关系,并将两者之间的关系进行表述的是著名的塔菲尔方程。
如上所述,从理论上考虑活化能和过电压之间的关系并将其与反应速率(电流)定量关联的方程为Butler-Volmer 方程。
