电流和反应速度介绍连载
本篇将介绍 平衡电极电位,有关电极反应动力学的极化和过电位的含义, 电流和电位的关系,标准速度常数的含义,传质过程的影响,电流与物质浓度的关系,电极反应的可逆性,以及存在均相化学反应的电极过程。最后介绍电极反应理论中的Butler-Volmer 方程的推导,高过电位近似和低过电位近似,以及电解液中的传质与电极反应的关系。
- 第一篇:平衡电极电位和电极反应动力学(1)
- 第二篇 电极反应动力学(2):电流和电位的关系
- 第三篇 电极反应动力学(3):标准速度常数
- 第四篇 电极反应动力学(4):(a)传质过程的影响 (b)电流与反应物浓度的关系
- 第五篇 电极反应动力学(5):(a)电极反应的可逆性 (b)当溶液中发生均相化学反应时
- 第六篇 电极反应理论(1): Butler-Volmer 方程的推导
- 第七篇 电极反应理论(2): Butler-Volmer 方程的高过电位近似和低过电位近似
- 第八篇 电极反应理论(3): 电解质溶液中的传质与电极反应
第一篇 平衡电极电位和电极反应动力学(1)
◆平衡电极电位
发生在单一电极上的简单电子转移反应(式1),其平衡电势Eeq可以用电解质溶液中所含的氧化态和还原态的浓度c(严格来说是活度a)通过能斯特方程(式2)来定量表示。
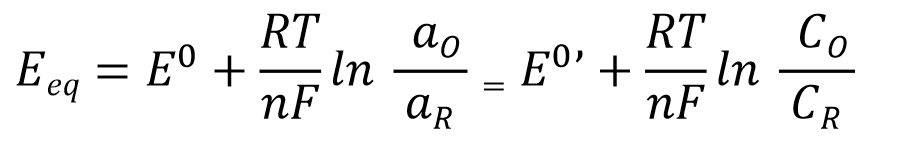
F:法拉第常数 (96485 C mol-1)
R: 理想气体常数 (8.31J K-1 mol-1)
T :绝对温度 (K)
E0:标准电极电位(standard electrode potential), aR = aO = 1 (标准温度)时的平衡电位
E0’:式量电位或条件电位(formal potential或conditionalpotential) 是基于浓度的标准电极电位。
Eeq:平衡电位 Eeq(根据参与反应的氧化-还原态物质的浓度比而改变的实验量)。
因此,平衡电位 Eeq是一个实验量,它可以根据参与反应的氧化还原物质的浓度比而改变。前面我们已经说明了,原电池的电动势可以使用能斯特方程从这些电活性物质的定量关系中计算出来。
◆电极反应动力学(1): 极化和过电位
当平衡被打破,可以看到反应开始向着一个方向进行时,该方向可以反映在电流的符号上(氧化电流为正,还原电流为负),例如,对于氧化反应为正反应的, 净反应速度V可以表示为氧化反应速度减去还原反应速度(式3)
这里,每个反应速度可以用反应物浓度 (mol cm-3) 与反应速度常数 k (cm s-1) 的乘积来表示,与均相反应体系的情况一样。那么 正向反应速度 Vox与逆向反应速度Vred可以表示为下面的式4和式5。
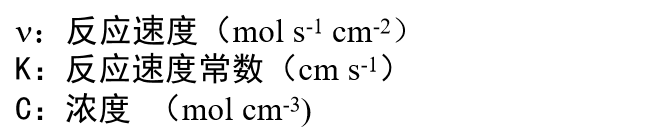
因为电流的绝对值与反应速度与成正比。氧化-还原电流和反应速率可以通过以下式6及式7的定量关系联系起来,观察到的净电流 I 可以表示为式8表示。
电位或电流 其中的一个可被用作控制变量,并对其进行主动改变,跟踪其他量如何响应这种变化,并做出理论解释。 这就是电化学测量方法的基本立场
顺便说一下,上述“使电位从平衡电位移动以引起反应”的操作和“由于反应而引起电位移动”的现象都用电化学中的术语“极化”来表示。 (偏离平衡电位的量称为过电压或过电位。)
其含义就是“要产生一定大小的电流,需要高于平衡电位的电压。”
当平衡电位以 Eeq 表示时,过电压 (符号为希腊字母 eta)为式9 定义的量。
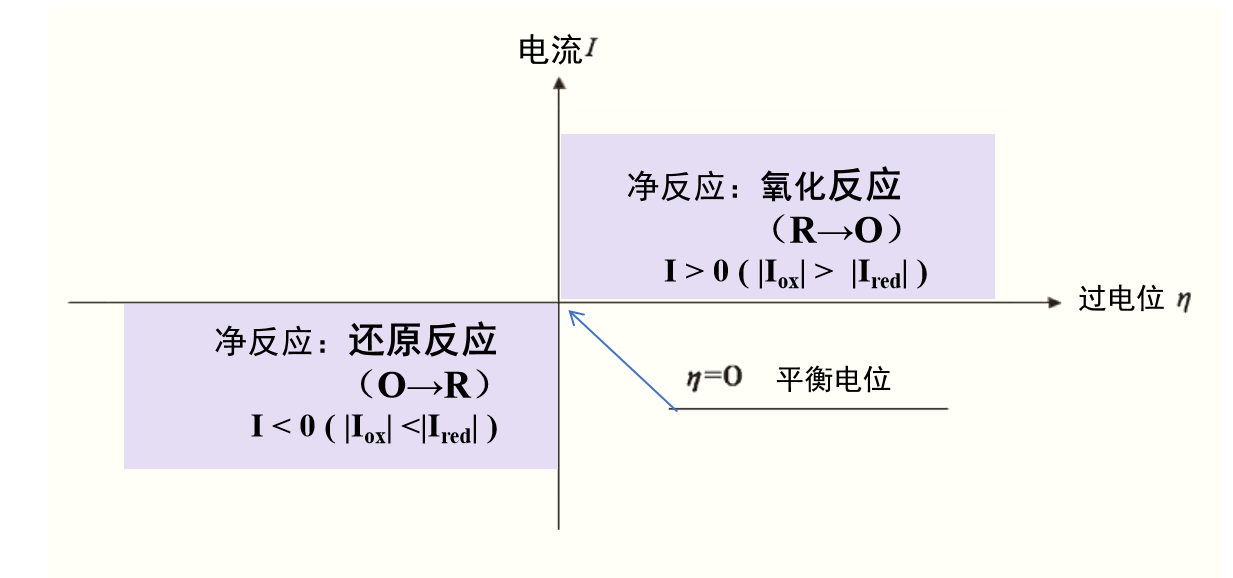
图1 过电位(超电势)和电流的关系
第二篇 电极反应动力学(2):电流和电位的关系
前面已经多次提及电流是表示反应速率的指标。 另一方面,可以说电势起到调节反应能量平衡的作用。 在均相化学反应中,放热反应或吸热反应是由反应物体系能量与产物体系能量的大小关系决定的。 类似地,在电化学反应中,是否可以将能量向外部输出(电池),或 是否需要从外部提供(电解)是根据反应物体系和生成物体系之间的能量差异来确定的。 在这里,让我们从能量的角度考虑电势对电极反应的影响。
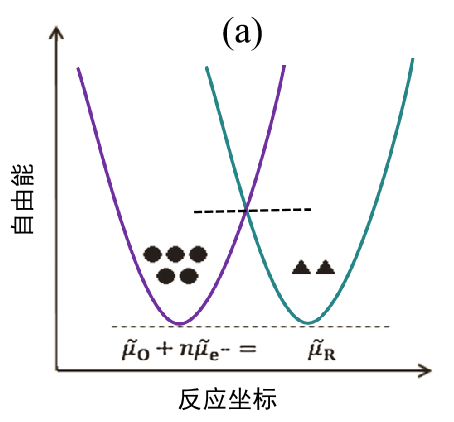
(a) 起始状态(平衡状态);
在平衡状态下反应物体系与产物体系的自由能相等。显然,反应不会向任何一个方向进行,所以 I = 0。 ● 和▲ 标记代表O 和R 的浓度大小。 请注意,平衡并不意味着浓度相等。
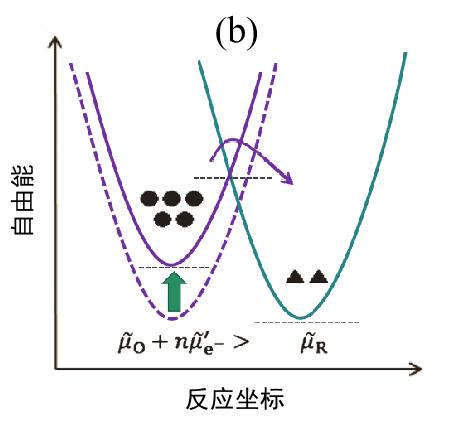
图 2. 电子转移反应能量示意图。
(b)施加负的过电压时(过渡状态);
对(a)的状态施加负的过电位时,电极内电子的能量增加,反应体系的自由能出现▣暂时性升高,O→R方向与R→O方向的反应活化能发生改变,反应向右侧进行而产生电流的流动(I < 0)
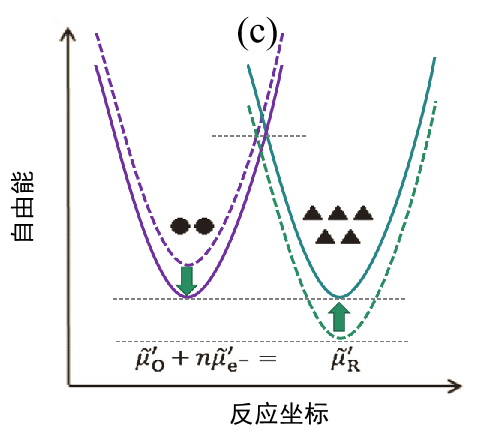
(c)最终状态(平衡状态)。
随着反应的进行,反应体系和生成体系之间的自由能差越来越小。 同时,活化能的差异也被消除,因此电流值减小,当 I = 0 时系统达到新的平衡。
从上面可以看出,当体系处于能量不稳定的非平衡状态(过渡态)时,可以观察到电流。
电化学反应的独特之处在于反应的方向可以通过施加在电极上的电位来控制。
当向电极施加与前一个相反方向的正过电位时,就会发生与上述相反的现象,此时反应从右向左进行,即氧化反应。 换言之,活化能的大小关系根据所施加的过电位的符号而反转。
与一般的化学反应类似,电化学反应的反应速度常数 k 是根据 Arrhenius 方程随活化能 Ea 变化的量。
(R :气体常数,T :绝对温度,A :系数)
根据上述关系,各反应速率常数表示如下。
最初通过实验发现了电解电流和外加电压之间的指数关系,并将两者之间的关系进行表述的是著名的塔菲尔方程。
如上所述,从理论上考虑活化能和过电压之间的关系并将其与反应速率(电流)定量关联的方程为Butler-Volmer 方程。
第三篇 电极反应动力学(3):标准速度常数
k0 标准速率常数(standard rate constant)
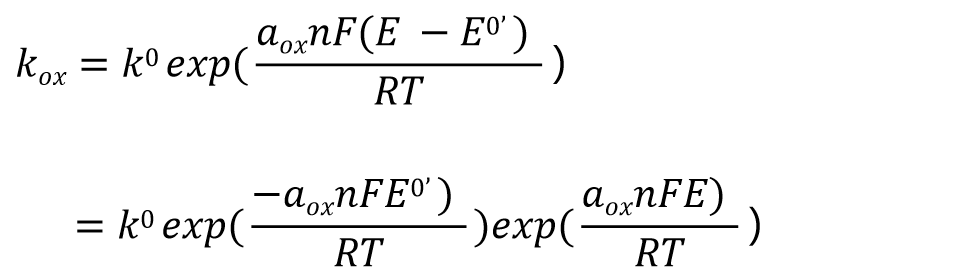
将上述方程的式21 与用于一般平衡电位的式(13)进行比较,那么Kox表示为式22, 并进一步变化成式23,进一步得到式24.
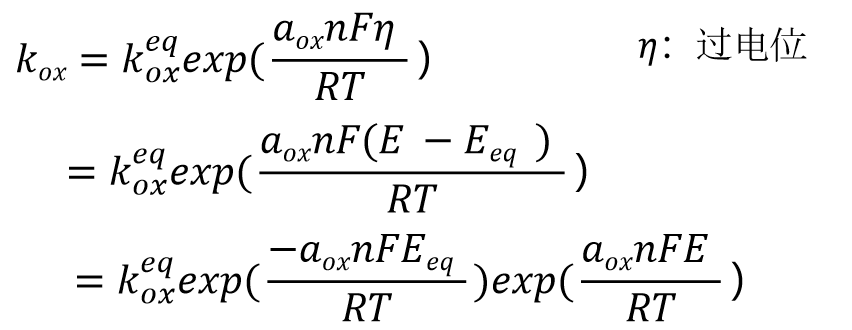
(22)
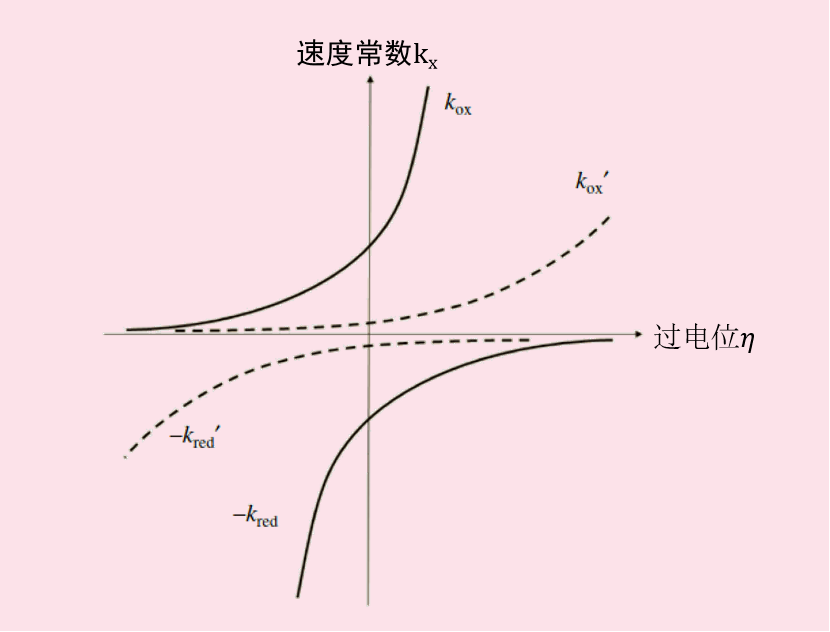
图 3. 反应速度常数与电位依存关系。
第4篇 电极反应动力学(4):(a)传质过程的影响 (b)电流与反应物浓度的关系
(a)传质过程的影响
然而,电极反应则是发生在空间有限的地方,叫做电极表面。那里 必须有反应物质的存在。 换言之,电化学反应是发生在电极与电解质溶液界面的非均相化学反应,随着反应的进行,除非不断地向界面提供新的反应物,否则反应就无法稳定地持续进行。
此外,还需要有一个从界面上将反应产物除去的过程。 这些物质的传输过程的问题总是与处理电化学反应相关(图 4)。

图 4. 电极反应过程示意图。
主要由电极界面上电子传递过程和物质传输过程组成。 注意,虽然图中没有画出,但在电子转移反应之前也有可能发生化学反应(先行化学反应CE)
传质过程有多种形式,这些将在下一个系列的连载中详细介绍。

图5 浓度过电位的概念图。
为此所需的过高的电压成分称为浓度过电压或浓度过电位。 当发生在电极界面的电子转移反应速度较大而溶液中的反应物传输供应跟不上时,就会出现浓度过电位的贡献,而此时活化过电位的贡献则相对较小。
如上所述,过电位有两种类型:活化过电位和浓度过电位。 如果电流在电极端子之间流动,则需要来自电解池(或电池)的内阻的额外电压分量(IR drop,ohm loss),但这本质上与电极反应无关。
第5篇 电极反应动力学(5):(a)电极反应的可逆性 (b)当溶液中发生均相化学反应时
(a)电极反应的可逆性
从反应动力学的角度来看,正向和逆向反应具有相同大小的速度常数的为可逆反应,正向和逆向的反应速度常数中的其中一个与另一个相比之下,极大或极小的,为不可逆反应。
如前所述,在电化学反应的情况下,原则上可以通过控制电极电位来改变正反两个方向的反应速率,似乎反应都能可逆地进行。 但是,对与实际反应会有各种限制存在,要做到这一点并不容易。 例如,电极作为催化剂的许多反应,例如水的电解,以及各种有机物氧化成二氧化碳,这些反应是不可逆的。电极被用作催化剂的许多反应,不能可逆地进行。
当在电化学中讨论“反应的可逆性”时,很难像一般化学反应一样直观地理解它。其原因仍然是由于电子转移过程与物质传输过程相结合,而进行一系列反应的特殊现象。一般来说,根据标准电子转移反应速率常数的大小,将电化学反应分为三类:可逆体系、半可逆体系和不可逆体系(不可逆系统)(见图6),电流的流动变化由于与物质传输速率的相对关系,其方式复杂,因此很难用一个词来解释这些特性。上述活化过电压和浓度过电压中哪一个占主导地位的问题,也与电极反应的可逆性密切相关。由于传质过程的影响取决于测量时间尺度,因此有必要首先了解质量传递过程,以了解可逆性。

图6 电极反应可逆性的概念图。
通过电子转移反应速率,传质速率的相对大小关系来说明。
图6 为电极反应可逆性的概念图。横轴表示传质速度,纵轴表示标准电子转移速度。对于标准电子转移速度和传质速度非常接近的半可逆体系而言具有以下特点:
・电流值由电子转移反应速度和物质传输速度共同决定。
・ 由于浓度过电压和活化过电压会因施加的电位和测量的时间尺度而变化,因此行为变得复杂。
・这种情况在实验中最为常见
对于电子传递速度远大于传质速度的体系为可逆体系, 该体系的电流值主要取决于传质速度,受浓度过电位支配。
・对于单纯的电子转移反应,电极表面上的氧化态还原态物质的浓度服从Nernst平衡。
再者,对于电子转移速度远小于传质速度的不可逆体系, 该体系的电流值主要取决于电子转移反应速度,受活化过电压的支配。

图7 当溶液中发生均相化学反应时的各种反应机理
在前一种情况下,从化学角度可以说反应是不可逆的,并且由于反向电子转移过程而产生的电流通常是观察不到的。在这些复杂的化学反应存在下,除了简单的电子转移过程外,电极表面的物质浓度受其影响很大,观察到的电流值也发生显着变化。在这种情况下,有必要在考虑反应机理的理论处理的基础上做出解释。
第6篇 电极反应理论(1): Butler-Volmer 方程的推导
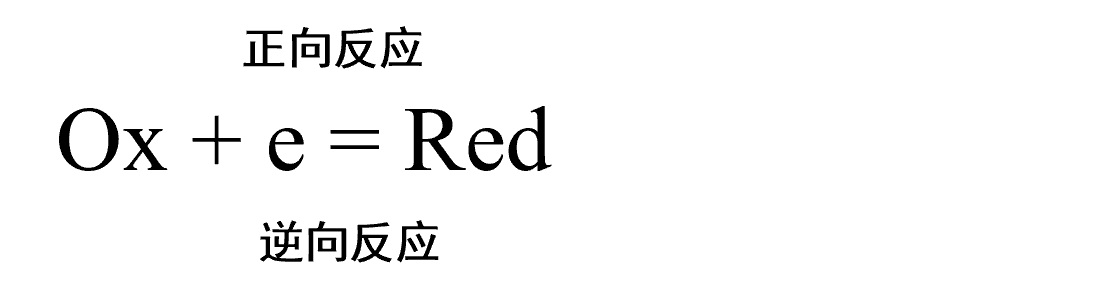
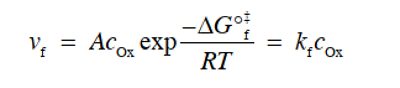
在图7(c)中,假设电势梯度可以线性逼近,从反应坐标的起始状态侧看,能量曲线的峰值在划分为α:1-α的位置。 此时,需要额外的活化能αFΔφ才能从初始状态到达能量曲线的顶部。 因此,此时的反应速率 vf 可以通过将式(26)中的 ΔG°‡f 改成ΔG‡f 来重新排列得到式28
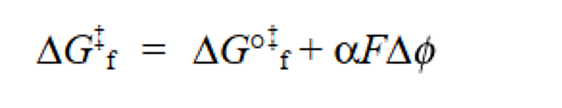
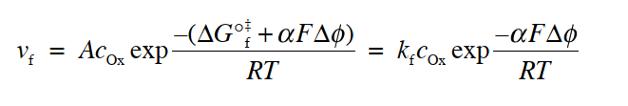
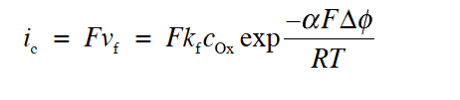
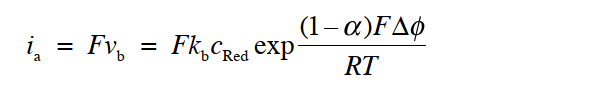
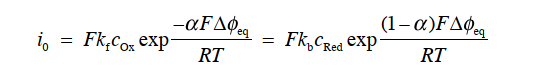
当有净电流流过电极电解质界面的情况下,当然此时的 ic不等于 ia。 按照惯例,将阳极电流为正,阴极电流为负,则净电流密度 i 可以用式32表示。
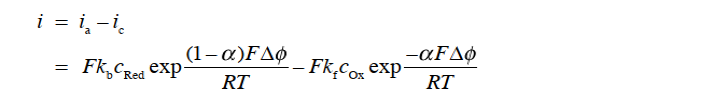
这种变化量称为过电位(over potential),其可以使用参比电极进行测量 式(33)。
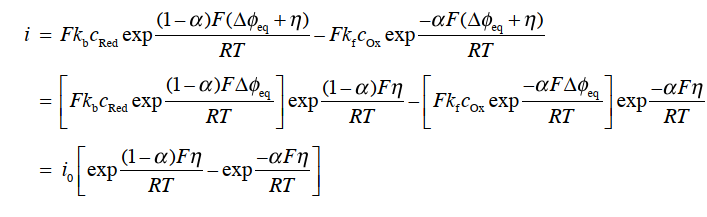
第7篇 电极反应理论(2): Butler-Volmer 方程的高过电位近似和低过电位近似
从Butler-Volmer 方程(式34)中可以看到,电极反应的净电流密度是由,表示阳极电流密度的 ia 和表示阴极电流密度 ic 的两项组成。
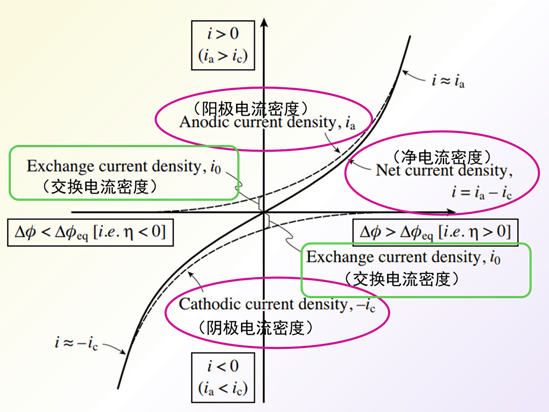
图 8 Butler-Volmer方程阳极电流密度 ia和阴极电流 密度ic(上,下虚线)和
净电流密度(实线) i =ia – ic相对于过电位 η (= Δφ – Δφeq) 的变化。
图8中的虚线表示阳极电流密度ia,阴极电流 密度ic 随过电位η的变化,为了便于区分,这里将阴极电流密度ic取负值表示。 图8中的实线表示了净电流密度i 随过电位η的变化。当η=0 时,反应处于动态平衡状态,此时的ic=ia ,用交换电流密度i0表示。
随着过电位η的增加,阳极电流密度ia增加而ic减少。 如果 η 足够大(具体而言,η> 0.10 V), 则可以忽略Butler Volmer方程中的阴极电流密度的ic项,近似处理后得到氧化反应净电流密度方程式 35。
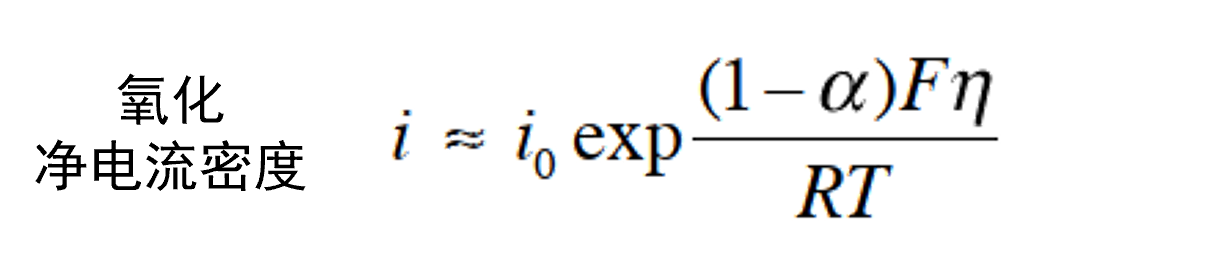
(35)
与此相反,当 η <–0.10 V 时, 则可以忽略ia 项。得到式36。
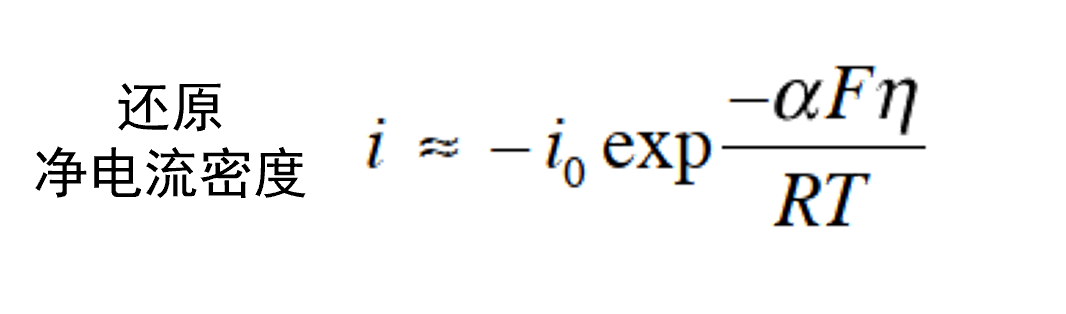
(36)
这两个方程被称为 Butler-Volmer 方程高过电位近似。
为便于作图,可将式(35)取两边的对数,变换后,得到过电位与logi 的关系式37。对于式(36),电流密度的绝对值| i | 可以用相同的方法进行处理。
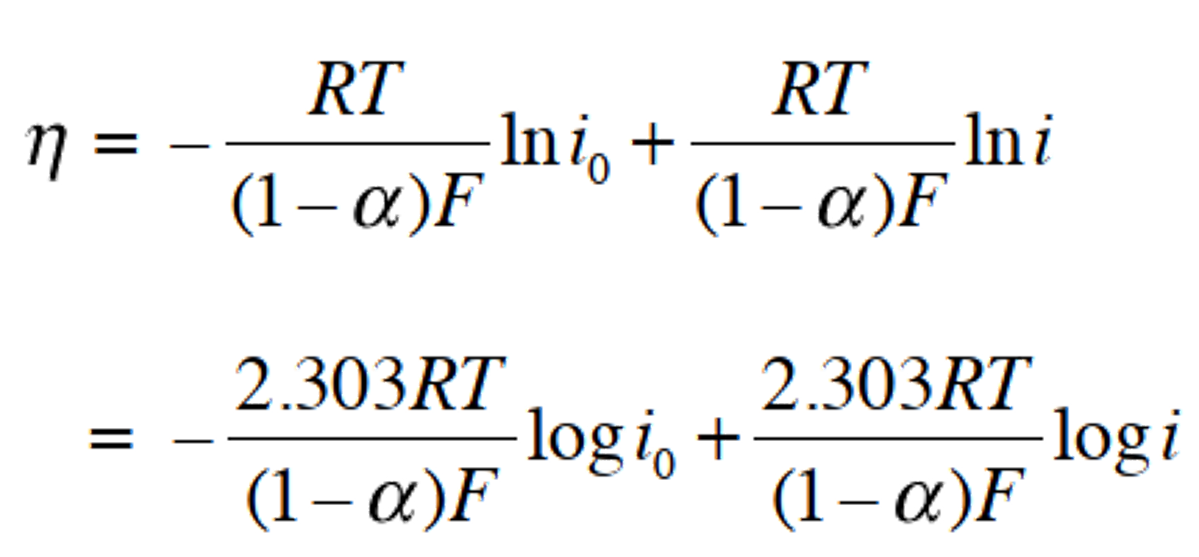
(37)
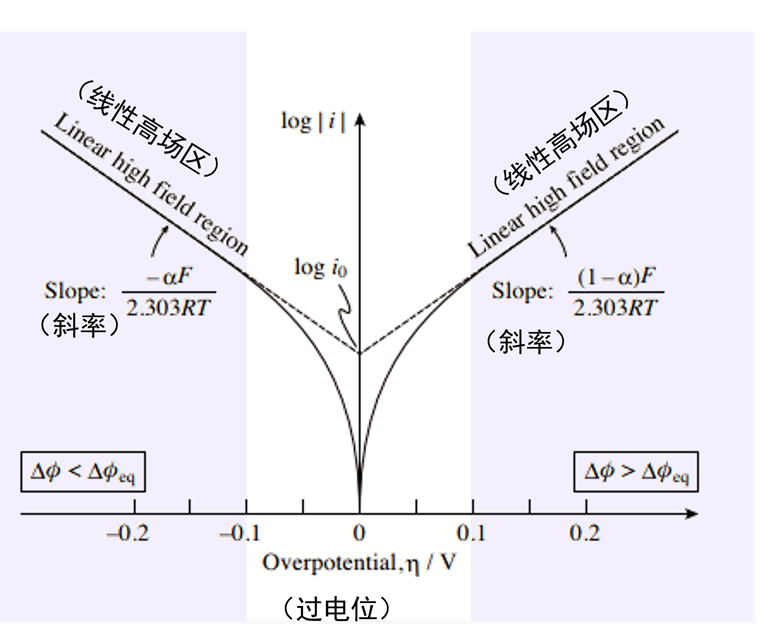
图 9 Tafel 方程的电流-电位曲线(log | i | - η ) 图 (n = 1) , 以及利用线性关系来确定 i0 和 α。
图 9表示了 η 和 log | i | 之间的关系,称为 Tafel 图。 直线部分(η <–0.10 V 和 η> 0.10 V 的部分)称为 Tafel 区域,log i0 和a值(n 电子反应情况下的 na 值)可以从这部分的截距和斜率估计。
现在的电化学,一般会将Tafel 方程(η = a ± b log | i |;a 和 b 为常数)称为 Butler-Volmer 方程的高过电位近似方程。但从历史上看,Tafel 是更早发现流过电极-电解质界面的电流与电极反应产生的过电位(电极电位)之间的关系。
考虑当过电位足够小时 (|η| <10 mV)的情况,将Butler-Volmer方程式,进行泰勒展开,并采用前两项 (expx ≈ 1+x) 得式38。
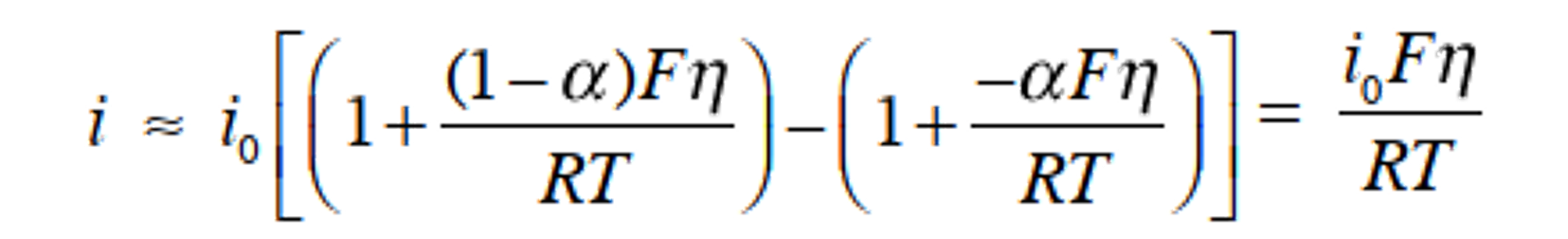
(38)
重写此式得到以下的式39。
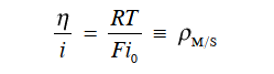
(39)
也就是说,当与平衡电位的偏差很小时(过电位很小),可以将类似于欧姆定律的东西应用于界面。式39的 比值η/i(=ρM/S)对应于界面对电极-电解质溶液界面处的电荷转移反应(也称为法拉第反应)的“电阻”,即极化电阻或电荷转移电阻)。 由于 ρM/S 主要取决于交换电流密度 i0,因此可以看作是一种“反应电阻”。 即ρM/S具有一定的电流密度(一定的电极反应速率)。它可以衡量驱动电极系统需要多少过电位的驱动力。
下面我们来看 交换电流密度 i0如何影响 η 与 i 曲线(极化曲线)。
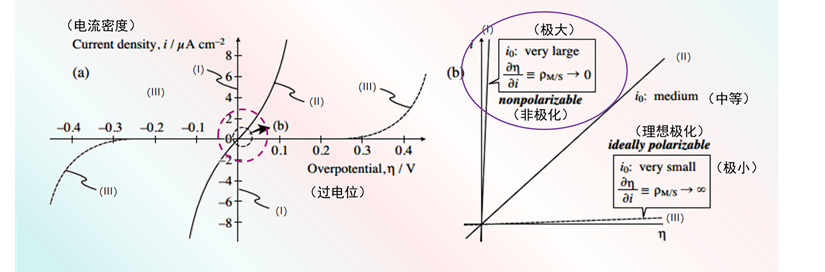
图 10 (a) 对于三种不同的交换电流密度 ((I) i0 = 1 mA cm–2, (II) i0 = 10–3mA cm–2, (III) i0 = 10–6 mA cm–2)
Butler -Volmer方程极化曲线(n = 1,α = 0.5)和(b)图(a)中低过电位区域的放大图(注: 曲线(I) 几乎与纵轴重叠)。
将其低过电位区域的放大后表示在图10(b)中(注:曲线I 几乎与纵轴重叠)。如果 i0 变得非常大,则 ρM/S 接近于零,极化曲线平衡电位附近的梯度接近无穷大。因此,跨界面的电位差Δφ与平衡时的电位差Δφeq基本相同。这样的界面称为非极化界面。
在另一个极端情况下,i0 无限小,ρM / S 变成无限大。此时仅有非常小的电流流过界面时,电位差Δφ会与Δφeq有很大的偏差。从不同的角度来看,即使η增加一点,电化学反应也几乎不会发生。这种界面称为可极化界面。
ρM/S和i0也是电荷转移反应速率的电位大小和极性的指标。图10 就是极化曲线的形状差异取决于i0的大小示意图。用于参比电极的体系必须具有非极化界面。这是因为希望电位差Δφ能稳定在一个定值。理想情况下,用于电池等储能设备的电极系统也应具有低极性。这是因为如果 ρM / S 大,则在充电/放电过程中会损失能量。
第8篇 电极反应理论(3): 电解质溶液中的传质与电极反应
电极反应是在两相,即电极和电解质溶液的界面上的非均相反应,为了使反应持续进行,附近溶液必须向界面方向进行物质(反应物和产品)的传输。例如,锌的电沉积(式39)反应,需要将溶液中的Zn2+离子从溶液本体中提供给界面,否则锌的电沉积无法进行。还有,对于Fe3+离子还原成Fe2+离子那样的反应(式40),如果产物也是能溶解在溶液中时,不仅必须向界面提供Fe3+离子,而且还必须不断地将产生的Fe2+离子从电极表面移除。
如果产生的Fe2+离子继续留在界面上,它们最终会超过溶解度并在界面附近沉淀出亚铁盐。 因此,溶液中的传质过程与电极反应过程一起在电化学反应中发挥着重要作用。
(40)
(41)
电解质溶液中离子转移的方式有扩散、对流、电泳三种方式,但对流的作用并不能到达电极附近,这部分的电解液基本处于静止状态。这个静止区域称为能斯特扩散层。其厚度δ取决于溶液的搅拌程度和粘度,一般在水溶液中为 10-2 到 10-3厘米左右。
此外,在许多电解质溶液中,是通过增加酸或盐的浓度来提高溶液的导电性和减小电泳的影响。 因此,扩散层内的传质就是它的名字上的含义,是受扩散支配的。
为简单起见,让我们考虑一个金属离子Mn+ 被还原成金属M的阴极电沉积反应(式42)。
(42)
在前面所述的电极反应理论中,是假设金属离子对电极表面的供应是充分的。 然而,实际上如果将过电位η,向负方向改变,使电极反应速度增加的话,反应物金属离子的供应就会出现延迟。使得电极表面上的金属离子浓度Cx=0,低于溶液的本体浓度C°。
此时,具有δ厚度的扩散层中的金属离子 浓度如图11所示,一般分成在扩散层中的线性变化和对流层中的平滑变化。
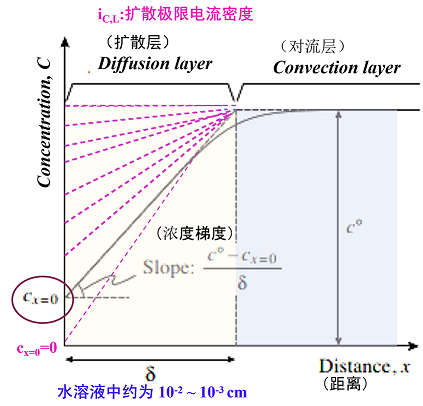
图11. 化学物质(体积浓度C°mol/L)在电极反应中被消耗时,在电极附近的有关化学物质的浓度分布和扩散层(厚度δ)的状态.
如果将一个线性近似的浓度梯度,代入扩散电流的菲克定律,电沉积引起的阴极电流密度ic可以表示为式43。式中的JD称为扩散通量,是在单位时间内跨越单位横截面的物质量(摩尔),将其乘以nF,可以转换为电流密度。 从式43中可以看出,最大的浓度梯度发生在cx=0=0时,此时扩散通量,也就是电流密度达到最大。这个电流密度被称为扩散极限电流密度ic,L,它是实际电解中η(负向)增加时,流动的阴极电流密度的上限。

(43)
扩散极限电流用式44表示。

(44)
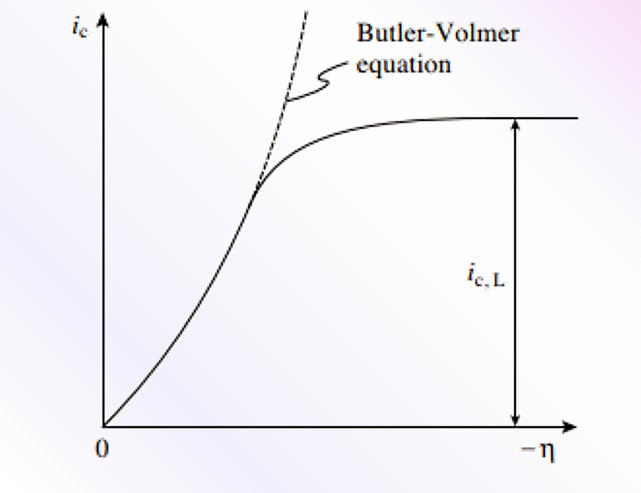
图 12 过电位向负方向变大,阴极电流达到扩散极限电流时的情况。
图 12 的阴极极化曲线中,如果将 η 向(负)逐渐增加时,Cx= 0 逐渐减小,在电流密度变为平台时,达到了阴极扩散极限电流密度 ic。
对于阳极电流密度ia 和它的极限电流密度 ia,可以做出完全相同的论证。
对于前面讨论的氧化还原反应,将传质影响加入Butler-Volmer方程后,极化曲线可以表示成式45。

(45)
