第十八篇 电化学阻抗谱(EIS)-(8)
Laboratory Of Research & Development, BAS Inc.
Professor Noriyuki Watanabe
Professor Noriyuki Watanabe
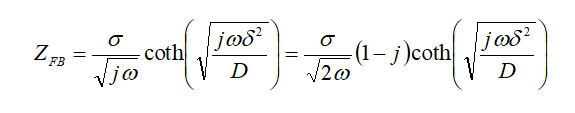
式18-1
图1显示了该等效电路的模拟结果。 电荷转移电阻(Rct)、双层容量(Cdl),有限膜厚度δ,扩散系数和浓度(如图所示),溶液电阻为零。当然,溶液电阻是存在的,但它只移动实轴上的位置,所以省略了。电荷转移过程的半圆之后,经过一定长度的45度梯度的直线,在低频带垂直于实轴上升。当有限膜厚度δ减小时,45度的直线就会变短。
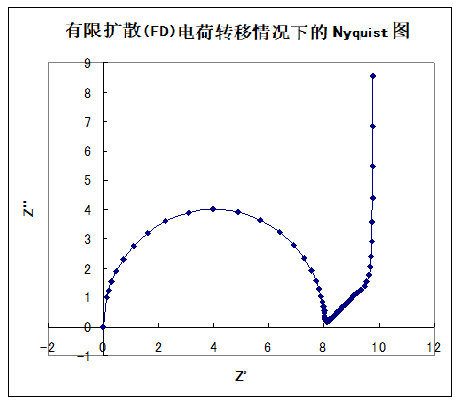
图18-1.有限扩散电荷转移情况下的奈奎斯特图
Rct(·)=8,Cdl(F/cm2)=0.0001,δ(cm)=0.1,
D=0.0001 cm2/s,C(mol/cm3)= 0.0001
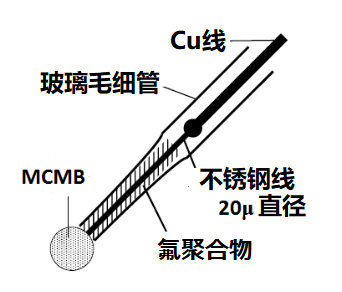
图18- 2 碳球电极(30µm直径)示意图
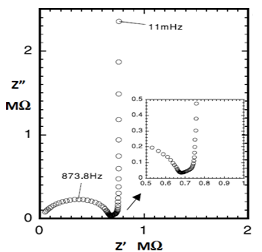 图18-3 锂离子嵌入微碳球电极的奈奎斯特图
图18-3 锂离子嵌入微碳球电极的奈奎斯特图
[18-1] Uchida et al.,Electrochimica Acta 47,885(2001)
[18-2]J.Newman et al.,J.Electrochem.Soc.147 293 0(2000)
[18-3] M.D.Levi et al.,J.Phys.Chem.B 108,11693(2004)
